5.9 Recall that particles in a liquid have a random motion within a close-packed irregular structure.
5.10 Recall that particles in a solid vibrate about fixed positions within a close-packed regular structure.
October 28, 2011
5.8 Boiling
Understand that a substance can change state from a liquid to gas by the process of evaporation or boiling.
If the temperature of liquid atoms increases even more the particles eventually have enough energy to break the inter-molecular bonds between the atoms, the particles now fly around at very high speeds (several hundred kilometers per hour) and fill any container they are placed in. this is the gaseous state. The state change between a liquid and a gas is called boiling.
If the temperature of liquid atoms increases even more the particles eventually have enough energy to break the inter-molecular bonds between the atoms, the particles now fly around at very high speeds (several hundred kilometers per hour) and fill any container they are placed in. this is the gaseous state. The state change between a liquid and a gas is called boiling.
5.7 Melting
Understand
that a substance can change state from solid to liquid by the process of
melting.
We know that all materials are made of atoms, in a solid state these atoms attract each other and are locked together by the inter-molecular forces between them. But, even in a solid state the atoms are not completely still; they still vibrate on a fixed position.
We know that all materials are made of atoms, in a solid state these atoms attract each other and are locked together by the inter-molecular forces between them. But, even in a solid state the atoms are not completely still; they still vibrate on a fixed position.
If these
atoms are given more internal (kinetic) energy, the particles vibrate faster
and further, if the temperature continues to increase to a point where the
inter-molecular forces between particles are not strong enough to hold the
structure together, but are strong enough to prevent the atoms from flying
apart from each other; a liquid is born. This process of going from a solid
state to a liquid is called melting or fusion.
October 23, 2011
5.6 Pressure Difference
Recall and use the relationship for pressure difference:

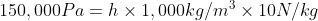
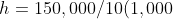)
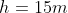


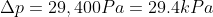
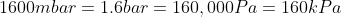
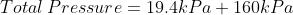
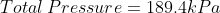
Δp =
pressure of the fluid (N/m2 or Pa)
h = Height of the fluid above loci (depth) (m)
ρ = density of the fluid (kg/m3)
g = gravitational field strength (N/kg)
h = Height of the fluid above loci (depth) (m)
ρ = density of the fluid (kg/m3)
g = gravitational field strength (N/kg)
Proof

- The bottom hole of this column squirts water the furthest
- This is because the water at the bottom has more pressure
- In the formula: Δp = hρg, ρ and g are both constant at all loci, but h is larger lower down \Δp = large.
Questions
The
pressure gauge on a submarine in a river was reading 100kPa when it was the
surface. If a sailor notices that the gauge is now reading 250kPa, how deep is
he? How would the answer change if he were diving in sea water that is slightly
denser that fresh water?
Note: ρfresh water = 1,000kg/m3
Note: ρfresh water = 1,000kg/m3
If the submarine
was in sea water he would be slightly shallower than 15m.
A diver
on Saturn’s moon Titan is 50m below the surface of a lake of liquid methane,
what is the increase in pressure on him due to his depth in the methane? The
density of liquid methane is 0.42g/cm3. The acceleration of gravity
on Titan is 1.4m/s2.
We are told that the pressure of the atmosphere on Titan is 1600mbar. What is the total pressure on the diver (in kPa)?
Note: 1000mbar = 1bar = 100,000Pa.
We are told that the pressure of the atmosphere on Titan is 1600mbar. What is the total pressure on the diver (in kPa)?
Note: 1000mbar = 1bar = 100,000Pa.
5.5 Equal Pressure
Understand
that the pressure at a point in a gas or liquid which is at rest acts equally
in all directions
Magdeburg
Hemispheres
When
the pressure inside the sphere is equal to the atmospheric pressure outside,
the hemispheres can easily be pulled apart because there is no external force
holding the hemispheres together, but if a vacuum is introduced inside the
sphere, the pressure atmospheric pressure pushing against the sphere is much
greater than the pressure pushing outwards, so the resultant force clamps the
sphere closed…
If
you’re confused… I tried my best to explain the pressure as a group of men.
1. No vacuum
There are 50 people inside the sphere trying to push the sphere open and 50 outside trying to keep it shut; obviously the sphere will remain in a stable state as neither side has more strength, but when 2 extra people are introduced (the people holding onto the handles) all of a sudden the side trying to open the sphere has more force than the opposing team. So the sphere comes loose and all the little people can escape.
2.
Vacuum
Inside the vacuum there are no longer 50 people inside trying to break open the sphere, but the 50 people outside (representing the atmosphere) are still there so the sphere remains firmly closed, and when 2 people are introduced to attempt to open the sphere, the sphere remains closed because those two people alone don’t have enough strength to fight against the 50 people working against them.
Inside the vacuum there are no longer 50 people inside trying to break open the sphere, but the 50 people outside (representing the atmosphere) are still there so the sphere remains firmly closed, and when 2 people are introduced to attempt to open the sphere, the sphere remains closed because those two people alone don’t have enough strength to fight against the 50 people working against them.
5.4 Pressure
Recall and use the relationship between pressure, force and area:
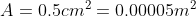
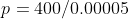
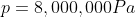
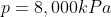
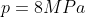
Clearly one can see that the high-heeled show will do the most damage to the floor.
NB: 1N/m2
= 1Pa
Using the
Formula
Calculate
the pressure generated by an ordinary shoe heel (person of mass 40kg, heel 5cm
x 5cm), an elephant (of mass 500kg, foot of 20cm diameter) and a high-heeled
shoe (person of mass 40kg, heel area 0.5cm2). Which ones will
damage a wooden floor that starts to yield at a pressure of 4000 kPa?
1. Ordinary shoe heel
2. Elephant
Clearly one can see that the high-heeled show will do the most damage to the floor.
October 6, 2011
5.3 Determining Density
Describe
how to determine density using direct measurements of mass and volume.
Density of a
regular solid
- Measure the mass using a balance
- Measure the width, length and height using a ruler
- Calculate volume (V = w x l x h)
- Calculate density (ρ = m/V)
Density of a liquid
- Measure mass of empty measuring cylinder using a balance
- Measure mass of liquid and measuring cylinder
- Subtract 1. from 2. to calculate the mass of the liquid
- Measure volume of liquid (using measuring cylinder)
- NB: measure to the bottom of the meniscus
- Calculate density (ρ = m/V)
Results:
Oil
- m = 15.74g
- V = 18.00cm3
- ρ = 15.74/18 = 0.87g/cm3
Density of an
irregular solid
- Measure mass using balance
- Measure volume using the ‘displacement’ method
- (submerge solid in ‘Eureka can’ and measure overflow)
- Calculate density (ρ = m/V)
Results: Stone
- m = 146g
- V = 42cm3
- ρ = 146/42 = 3.5g/cm3
5.2 Density
ρ
= Density [kg/m3] or [g/cm3]
m = mass [kg] or [g]
V = Volume [m3] or [cm3]
m = mass [kg] or [g]
V = Volume [m3] or [cm3]
NB:
ρ = rho (Greek letter)
1kg = 1000g
1m = 100cm
1m3 = 100,000cm3
1g/cm3 = 1000kg/m3
ρ = rho (Greek letter)
1kg = 1000g
1m = 100cm
1m3 = 100,000cm3
1g/cm3 = 1000kg/m3
Topic 5 Solids, Liquids and Gases Keywords
- Absolute Zero: The lowest possible temperature. 0K = -273°C.
- Brownian Motion: The slow, random motion of large, visible particles such as smoke particles. Explained by postulating much smaller, faster particles that are not visible, such as air particles, that collide with the large particles and make them move.
- Density ρ, (g/cm3) or (kg/m3): The mass, in kilograms, of one metre cubed of a substance.
- Diffusion: Molecules moving from an area of high concentration to an area of low concentration.
- Flexible Container: A container that changes its shape depending on the pressure inside or outside it. The volume is variable and the pressure is constant. Examples are syringes and pistons.
- Ideal Gas: A theoretical model of a gas that describes gas molecules by using the Kinetic Theory. The molecules are assumed to collide elastically with the walls of the container they are in.
- Kelvin (K): The units of absolute temperature. 273K = 0°C
- Kinetic Theory/Particle Model: A model of solids, liquids and gases that explains the observed properties of the materials by postulating that they are made up of lots of tiny, hard, incompressible spheres. At higher temperatures the spheres move faster.
- Mass (kg): Amount of material in an object, measured in kilograms
- Pressure (Pa) or (N/m2): The effect of a force spread out over an area. Pressure = Force/area, p=F/A
- Rigid Container: A container that will keep a fixed shape regardless of the pressure inside or outside it. The volume is constant and the pressure is variable. Examples are rigid metal cans and glass bottles.
- Volume: The space occupied by an object in three dimensions measured in m3, For cuboids, V = l x h x w.
October 4, 2011
Energy Formulae summary
Here is a list of all the formula mentioned in this topic:
)
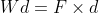
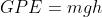
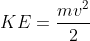
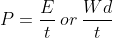
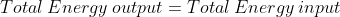
Quantities
and Units
- Energy = Joules (J)
- Wd = Work done (J)
- GPE = Gravitational Potential Energy (J)
- KE = Kinetic Energy (J)
- F = force (N, Newtons)
- d = distance moved in the direction of the force (m, metres)
- m = mass (kg)
- g = gravitational field strength (N/kg) NB: G on earth = 10N/kg
- h = height (m)
- v = velocity (m/s)
- P = power (W, Watts)
- t = time (s)
End of Energy Topic
4.17 Energy Advantages
Describe
the advantages and disadvantages of methods of large-scale electricity
production from various renewable and non-renewable resources.
Energy Source
|
Advantages of Use
|
Disadvantages of Use
|
Fossil Fuels
|
Fuels readily available, easy to make electricity.
|
Fuels are non-renewable, produce C02 and
so add to global warming, acid rain. Oil spills damage environment.
|
Nuclear
|
Creates large amounts of energy, is reliable and
relatively cheap to set up. Produces no C02.
|
Expensive to decommission power stations after use.
Waste is produced that is dangerous for long periods. Reactors that are not
cooled will overheat and release waste.
|
Wind
|
Produces no C02. Once setup takes little
maintenance. Renewable.
|
Expensive to set up. Installations may be noisy and
seen as ugly. Unreliable as you cannot count on the wind all the time.
|
Wave
|
Produces no C02. Small devices can produce large
amounts of electricity. Out to sea means out of sight. There are large areas
unused across the globe. Renewable.
|
Easily destroyed by bad weather. Electricity
produced needs to be transferred over long distances. Expensive to set up.
|
Tidal
|
Reliable as the tides are predictable as they depend
on the Sun and Moon.
Produces no C02. Renewable. |
Few areas are suitable of being dammed. The dam
restricts movement of sea life. Silt will build up. tides vary in strength
throughout the day. Expensive to set up.
|
Hydroelectric
|
Produce no C02. Once set up have little
maintenance cost. Create useful water resources. Can be turned on and off
instantly. Renewable.
|
Expensive to build. Destroy ecosystems. If dams
break damaging flooding will occur. Most areas in the world that can be used
are being used.
|
Geothermal
|
Virtually emission free. Some reduce sulphur
emissions. Simple systems are easy to maintain. No fuel costs. Renewable.
|
Expensive to set up. Expensive drilling through hot
rocks. Limited areas in the world where hot areas are close to the surface.
|
Biomass
|
Produces no long term C02. Renewable as trees can be
regrown
|
Limited areas of land available. Reduces the
production of food.
|
Solar Heating
|
Produce no C02. Renewable. Light is free.
|
Unreliable as the sun does not shine all the time.
No sun at night.
|
Solar (Photovoltaic) Cells
|
Produce no C02. Renewable. Light is free.
Can be small to be used instead of batteries.
|
Unreliable as the sun does not shine all the time.
No sun at night. Expensive to set up.
|
4.16 Generating Electricity
Understand
the energy transfers involved in generating electricity using:
- Wind
- Water
- Geothermal resources
- Solar heating systems
- Solar cells
- Fossil fuels
- Nuclear power
Wind power stations
Fossil Fuel power stations
Hydroelectric power stations
Geothermal power stations
Solar Heating system
Solar Cell
Nuclear power stations
Subscribe to:
Posts (Atom)











